Sudoku Solving Algorithm

Introduction

The Problem

Sudoku is a logic-based number placement puzzle consisting of a 9×9 grid divided into nine 3×3 subgrids. The puzzle begins with some cells pre-filled with numbers. To solve the puzzle, each row, column, and 3×3 subgrid must contain all digits from 1 to 9 without repetition.

Objective

The goal was to develop a Python-based Sudoku solver capable of handling puzzles ranging from very easy to hard, with a focus on efficiency and optimization.

Algorithm Description

I implemented constraint propagation through a backtracking Depth-First Search (DFS) algorithm. To reduce the branching factor, the algorithm uses the minimum-remaining values (MRV) heuristic by prioritizing sudoku cells with the fewest possible options.

Core Algorithm

• Depth-first search with backtracking
• Forward checking to detect invalid states early

Constraint Propagation Techniques

• Arc-consistency algorithm to reduce variable domains before search
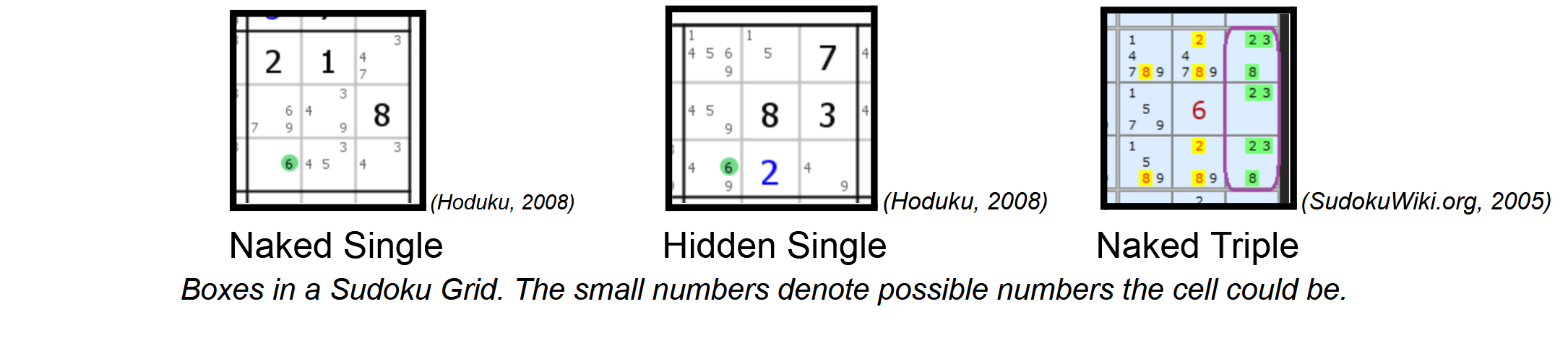
• Naked singles (when a cell has only one possible value)
• Hidden singles (when only one cell in a unit can contain a specific value)
• Naked sets (pairs, triples, quads)

Selection Heuristics

• Minimum Remaining Values (MRV) to choose which cell to fill next
• Randomized selection among equal candidates to avoid getting stuck

Implementation Details

The algorithm's strength lies in its extensive use of constraint propagation before and during the search process. By significantly reducing the domain of variables before initiating DFS, the search space becomes much more manageable.

I was inspired by Deep Blue's chess-specific knowledge and attempted to incorporate as many sudoku-specific constraints as possible. Unfortunately, time constraints prevented implementing more advanced techniques like the Phistomefel Ring, which remains a goal for future work.

Results and Performance

The algorithm currently solves:

• Hard puzzles in approximately 200-300ms on average
• What previously took minutes now completes in tenths of a second

The biggest performance improvement came from the arc-consistency implementation of iteratively checking for naked singles, which made solving hard puzzles feasible. The MRV heuristic also decreased solution time by reducing the branching factor of the search tree.

Optimizations and Complexity

The time complexity of the DFS algorithm is O(b^m), where b is the branching factor and m is the maximum depth. Through various optimizations and heuristics, I was able to:

• Significantly reduce the branching factor using MRV
• Decrease the number of nodes in the search tree with sudoku-specific constraints
• Detect invalid states early with forward checking

In terms of programming, the code was not fully optimized due to my inexperience. Future improvements could include using NumPy to vectorize array operations, which could potentially reduce execution time further.

Reflections and Future Work

While my solver doesn't match the ~20ms performance of some professional solvers, the improvement from minutes to hundreds of milliseconds represents significant progress. The experience demonstrated the power of combining general search algorithms with domain-specific knowledge.

For future enhancements, I plan to:

• Experiment with the "Dancing Links" algorithm for more efficient constraint satisfaction
• Implement additional interesting sudoku-specific techniques like "x-wing" and the Phistomefel Ring
• Optimize code execution with NumPy vectorization
• Explore more advanced search algorithms and heuristics

References

• Hoduku (2008). HoDoKu: Solving Techniques - Singles (Hidden Single, Naked Single, Full House). hodoku.sourceforge.net
• Mastering Sudoku (2024). Phistomefel Ring Explained & How To Solve Sudokus With It. masteringsudoku.com
• SudokuWiki.org (2005). Naked Candidates. sudokuwiki.org